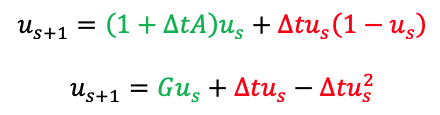This is probably a very basic question, but it's been about 8 years since I've taken PDEs or linear algebra so I'll ask anyway. I understand how we represented the diffusion equation using a linear operator in Lecture 13, but I'm struggling to do the same thing with the KPP-Fisher equation in assignment 5 because of the quadratic term on the right hand side. I have been trying to represent the equation as a single matrix operating on a vector like we did on slides 19 / 20 of Lecture 13 but so far I can't figure it out.
My other idea was to have a matrix operator that accounts for the discrete spatial 2nd derivative like we did for the diffusion equation but keep the non-linear term as a separate operation. Something like the attached image, where u is a vector, A is the discrete spatial 2nd derivative, and "1" would be the identity matrix:
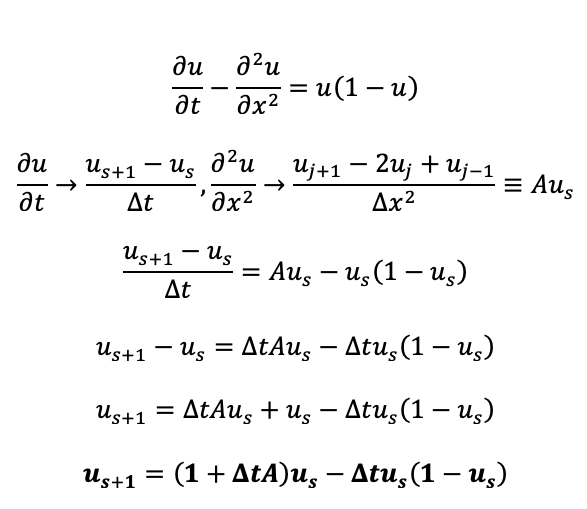
I'm not sure if I'm on the right track here so any pointers would be appreciated.