Assignment 5

Due date: Thursday, October 24th at midnight (Thursday night).

An organism is called diploid if members of the species, such as humans, possess two copies of each gene. Offspring of such species are given a single copy of each gene from each parent. If a particular gene has two possible alleles, \(A_1\) and \(A_2\), then an individual of the population is called homozygous if he possesses two copies of a single allele, meaning either \(A_1 A_1\) or \(A_2 A_2\). Alternatively, if an individual possesses both alleles, \(A_1 A_2\), she is called heterozygous.

The phenomenon of Random Genetic Drift occurs when a small population of individuals is isolated from a larger population, and the population continues to breed. The resulting population's genetic distribution can become skewed, relative to the original population, resulting in the disappearance of a heterozygous population. We will explore this phenomenon in this assignment.

Let us propose the following situation: suppose a purely heterozygous population, all with alleles \(A_1 A_2\), is isolated from a large population for some reason. Let us propagate this smaller population of individuals, keeping the population constant, with each generation of offspring descended from different parents. We will then examine what happens to the distribution of genotypes as the generations proceed.

0) You must use version control ("git"), as you develop your code. We suggest you start, from the Linux command line, by creating a new directory, e.g. assignment5, cd into that directory and initialize a git repository ("git init") within it, and perform "git add ..., git commit" repeatedly as you add to your code. You will hand in the output of "git log" for your assignment repository as part of the assignment. You must have a significant number of commits representing the modifications, alterations and changes to your code. If your log does not show a significant number of commits with meaningful comments you will lose marks.

1) Create a file named Drift.Utilities.R containing the following functions.

1a) Write a function whose purpose is to create a data frame of \(n\) rows and two columns: "gene1" and "gene2". The columns correspond to the two copies of a gene that each individual in the population has, and each row represents an individual of the population. The function should initialize the genes of the individuals to a heterozygous state, and return the data frame. You may represent the different alleles however you desire. The rep() function might be helpful here.

1b) Let us assume that a child will receive a copy of allele \(A_1\) from his parent with some probability \(p\). Write a function that, given the probability \(p\), randomly selects and returns the allele that the child receives from that parent. The sample() function may be helpful here.

1c) Write a function which, given a population (in the form of a data frame), will calculate the genes of each member of the next generation. The function should perform the following steps:

• Pick two parents. You may do this in order. The seq() may be helpful. For each parent:
• Calculate the probability of a child getting allele \(A_1\) from that parent, assuming an equal probability of getting either gene that the parent has.
• Randomly calculate the gene that the parent's child receives from that parent.
• The two genes that each child receives from her parents should be stored in a new data frame. The rbind() function may be helpful here.
• Each pair of parents should have two children, so that the population of each generation is constant.
• The individuals in the new population data frame should be randomized, so that the parents are randomized for the next generation.

The population of the next generation should be returned by the function.

1d) Write a function which, given a population, calculates the fractions of the population which are \(A_1 A_1\), \(A_2 A_2\), and \(A_1 A_2\), and returns these values. Note that \(A_1 A_2\) is the same as \(A_2 A_1\).

1e) Write a function which, given a population size \(n\) and number of generations \(m\)

• Creates a heterozygous population of size \(n\).
• Calculates the next generation of the population, \(m\) times.
• For each population, including the initial population, the fraction of the three genotypes should be calculated, and stored.

The fractions of the three genotypes, for each population, should be returned.

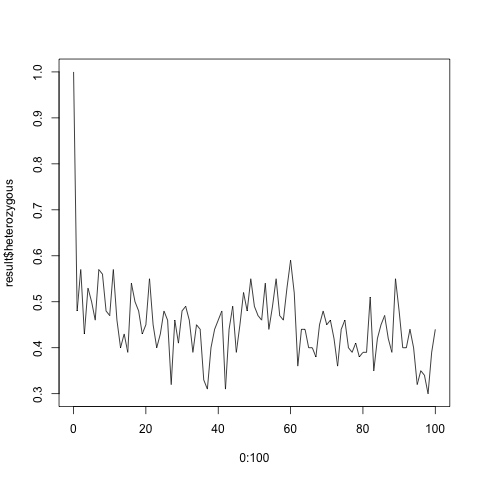
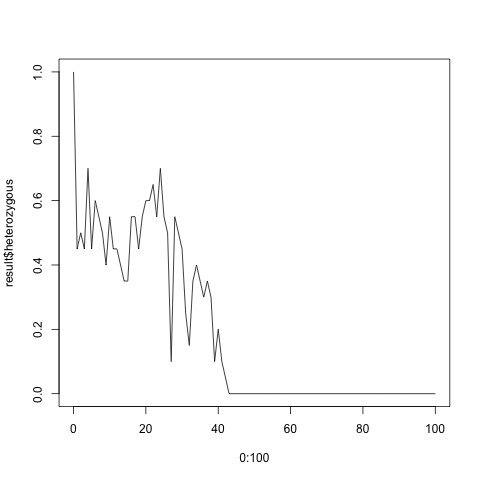
Running the code generates quite different results depending on the size of the population. If you have 100 individuals, the fraction of the heterozygous population settles around 0.5. For 20 individuals the heterozygous population eventually disappears altogether, and the population becomes homozygous.

>
> source("Drift.Utilities.R")
>
> fractions <- sim.many.generations(100, 100)
> fractions2 <- sim.many.generations(20, 100)
>
> plot(0:100, fractions$heterozygous, type = 'l')
> plot(0:100, fractions2$heterozygous, type = 'l')
>

2) Create an R script called Drift.Analysis.R that will perform the following steps:

1. sources your utilities file Drift.Utilities.R,
2. takes an argument from the command line, the size of the population, \(n\).
3. simulates the evolution of an initially heterozygous population of size \(n\), for 100 generations.
4. creates a plot of the fraction of the heterozygous population, as a function of generation.
5. If the command-line argument not numeric the script should exit with an appropriate error message. Converting the argument to numeric, using the as.numeric() function, and then checking to see if it's not a number, using the is.na() function, is a good approach.
6. If the value of the command-line argument does not make sense the script should exit with an appropriate error message.  Amongst other conditions, the command-line argument should be an even number.
7. If the number of command-line arguments is not 1 the script should exit with an error message.

Note that this script will generate an "Rplot.pdf" file when you run it from the bash prompt. This file contains the plot your script generated.

Note that, starting with this assignment and for the rest of the semester, you will be expected to use coding best practices in all of the work that you submit. This includes, but is not limited to:

• Plenty of comments in the code, describing what you have done.
• Sensible variable names.
• Explicitly returning values, if the function in question is returning a value.
• Not using the print() function to return values.
• Proper indentation of code blocks.
• No use of global variables.
• Using existing R functionality, when possible.
• Creating modular code. Using functions.
• Never copy-and-pasting code!

Submit your Drift.Utilities.R and Drift.Analysis.R files, and the output of git log from your assignment repository.

Both R code files must be added and committed frequently to the repository. To capture the output of git log use redirection (git log > git.log, and hand in the git.log file). 

Assignments will be graded on a 10 point basis. Due date is October 24th 2024 (midnight), with 0.5 penalty point per day off for late submission until the cut-off date of October 31 2024, at 10:00am.