Assignment 7

Due date: November 10, 2022 at 11:59 pm.

Be sure to use version control git, as you develop your script. Do git add and git commit repeatedly as you add to your script. You will hand in the output of git log for your assignment repository as part of the assignment.

Data

For this assignment, let us again consider the histogram that we created as part of Assignment 5.

>
> source("../assignment5/Circle.Utilities.R")
>
> diffs <- sim.null.hypo(5, 10000)
>
> hist(diffs, breaks = 21, freq = FALSE)
>

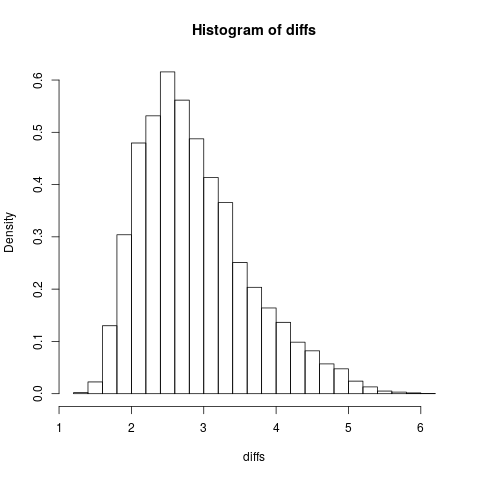
As you can see, this distribution is neither symmetric nor Gaussian. As such, the mean is not the most-probable value. If we're interested in the most-probable value (the 'mode', see lecture 10, slide 13), or getting confidence intervals on this value, we will need to use bootstrapping.

Problem

As usual, create a utilities file to contain your functions.

1a) Create a function which, given a vector of (continuous) numeric values, will return the most-probable value. I suggest, as we did in Assignment 5, you use the hist function, and use the mid-point of the bin.

Note that the mode function that comes with R does not return the 'mode' in the sense of lecture 10, slide 13. Also note that the examples of 'mode' functions that you will find online are for discrete variables, not continuous as we have in this case, and as such will be wrong if you use them. Write your own!

1b) Create a function which will take a vector of numeric values, and an integer n as arguments. The function will perform nonparametric bootstrapping on this data, n times, calculating the most-probable value of the data set. The function should return the output of the boot command.

1c) Create a function which takes three integers as arguments. The first argument will indicate the maximum value of k, the number of birds, to evaluate; the second will be the number of artificial data to generate, m; the third will be the number of bootstrap iterations to run, n. The function should generate m artificial maximum angular differences, as we did for the Null Hypothesis in Assignment 5, for each appropriate integer value of k up to the first function argument. Nonparametric bootstapping should be applied to each artificial data set, using n replicates. For each value of k the value of the test statistic, as calculated by bootstrapping, should be returned, as well as the upper and lower 95% confidence intervals calculated using "BCa".

Your driver script should perform the following steps.

1. It should take a single command line argument, indicating the maximum value of k to evaluate.
2. It should perform nonparametric bootstrapping, 2000 times, on 1000 maximum angular differences, generated as we did for the Null Hypothesis in Assignment 5, for each value of k up to the maximum k value.
3. It should plot the value of the test statistic versus k. On this plot it should also add the upper and lower 95% confidence interval.

Some notes to follow when implementing your script:

1. You will need to source Circle.Utilities.R. Do NOT source it as on this page, up above. Copy your Assignment 5 Circle.Utilities.R to your Assignment 7 directory, and source it there. (If your code for 1a and 1b of Assignment 5 did not work properly, fix it!). If you source it as above your code will likely not work for the graders and you will lose marks.
2. Be sure to defend your command line argument for your driver script against all possible failure modes.

Submit your Circle.Utilities.R, new utilities file, driver script and the output of git log from your assignment repository.

To capture the output of git log use redirection, git log > git.log, and hand in the git.log file.

Assignments will be graded on a 10 point basis. Due date is November 3rd, 2022 at 11:59pm, with 0.5 point penalty per day for late submission until the cut-off date of November 10, 2022 at 9:00am.