Assignment 6

Due date: Thursday, October 28th at midnight (Thursday night).

0) Be sure to use version control ("git"), as you develop your code. We suggest you create a new directory to hold this assignment, "assignment6" for example, and initialize a new git repository within it. Do "git add ....,  git commit" repeatedly as you add to your scripts.  You will hand in the output of "git log" for your assignment repository as part of the assignment. You must have a significant number of commits representing the modifications, alterations and changes in your scripts. If your log does not show a significant number of meaningful commits you will loose marks.

This assignment will explore a variation on the Birthday Problem. The problem is simply put: what is the probability of two random people in a room having the same birthday, if there are n people in the room? In our variation of this question we will examine the Three-Birthday Problem: what is the probability of three random people in a room have the same birthday, if there are n people in the room?

1) Create a file named Birthday.Utilities.R. It will contain the functions described in part 1 of the assignment.

1a) Create a function called sample.n. This function takes one mandatory argument, n, the number of people whose birthdays will be randomly picked.  The function will also take an optional boolean argument, whose default value will be FALSE.  If the boolean argument is FALSE the birthdays of n people will be randomly sampled, with equal probability, between 1 and 365, and returned as a vector.  If the boolean argument is TRUE then the attached file, bdata.txt, will be read in.  This file contains the distribution of birthdays from a real sample of people.  The birthdays from February 29 will be ignored.  The birth counts for the remaining 365 days will then be used to determine the actual probability of being born on a given day.  These probabilities will be used to modify the probabilities used by the sample function, and the birthdays of n people will then be sampled using these actual probabilities.  This vector birthdays will then be returned by the function.

1b) Create a function called check.three.birthdays. This function will take single argument, a vector of birthdays.  This function will determine if there is at least one case of exactly three people have the same birthday.  If there is the function will return TRUE; if not it will return FALSE.

1c) Create a function called check.n.birthdays. This function will take single argument, n, the number of people.  It will randomly generate birthdays for those n people, using equal probability, and return a boolean value indicating whether any three of the people share a birthday.

1d) Create a function called avg.n.birthdays.  This function will take two arguments, n, the number of people, and m, the number of times to repeat the calculation.  Using one of the *apply functions, this function will check whether there is at least one case of exactly three people in n sharing a birthday (when generated using equal probability), and will repeat this calculation m times.  It will then return the calculated average probability that there is a case of exactly three people in n sharing a birthday.

1e) Create a function called avg.many.n.birthdays. This function takes two arguments, n, the maximum number of people, and m, the number of times to repeat the calculation.  Using one of the *apply functions, this function will calculate and return the average probability that there is a case of exactly three people in n sharing a birthday (when generated with equal probability), for the number of people ranging from 1 to n.  These averages will be calculated by repeating the calculation m times.

Note that, if you want to use an *apply function, but the function the *apply function is calling takes more than one argument, you can pass additional arguments by listing them after the name of the function:

> sapply(rep(1, 10), rnorm, mean = 10)
[1] 11.323774 10.242815 12.010001 9.373534 11.194652 9.562051 8.166936
[8] 10.242222  9.198814  9.437305
> 

1f) Create a function called run.chisq.test. This function takes one argument, n, the number of birthdays.  The purpose of this function is to determine whether or not birthdays sampled using the probabilities from the real data set can be distinguished from an equal-probability distribution.  This function should sample n birthdays using the probabilities determined from the data file.  It should then recast the data into a form the chisq.test will accept, and return the output of the test.

2) Create an R script, named Run.Birthdays.R, which:

• sources the file "Birthday.Utilities.R"
• reads an argument from the command line.
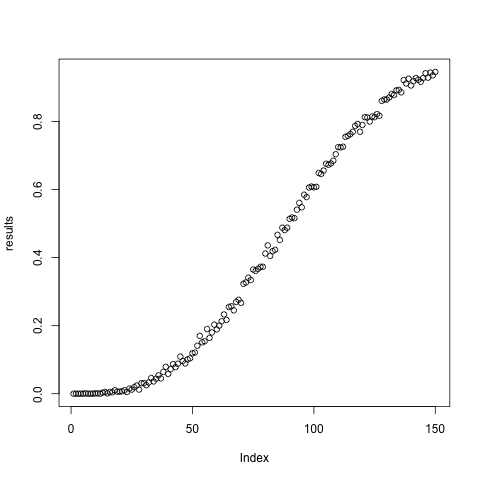
• If the argument is "MakeProbPlot" the script calls avg.many.n.birthdays for a maximum of 150 people, repeated 1000 times. It will then plot the results, using the 'plot' function, and write a nice sentence describing what it is doing. Note that, because this is an R script, the plot will automatically be placed into a file called Rplot.pdf.
• If the command-line argument is "ProbTest", the script calls run.chisq.test for 10000 people. If the p value of the test is less than 0.05 it will print out something like "The null hypothesis that the probabilities for each birthday are the same is rejected, with a p value of ...". If the p value is greater than 0.05 it will print out a similar, though opposite, sentence.
• If the command-line argument is neither of the above the script should exit with an appropriate error message.
• If the number of command-line arguments is not 1 the script should exit with an error message.

Your plot of calculated average probabilities should look something like this:

Note that, starting with this assignment and for the rest of the semester, you will be expected to use coding best practices in all of the work that you submit. This includes, but is not limited to:

• Plenty of comments in the code, describing what you have done.
• Sensible variable names.
• Explicitly returning values, if the function in question is returning a value.
• Not using the print() function to return values.
• Proper indentation of code blocks.
• No use of global variables.
• Using existing R functionality, when possible.
• Creating modular code. Using functions.
• Never copy-and-pasting code!

Submit your Birthday.Utilities.R and Run.Birthdays.R files and the output of "git log" from your assignment repository.

Both R scripts must be added and committed frequently to the repository. To capture the output of 'git log' use redirection ( git log > git.log, and hand in the "git.log" file).